Il concetto di rischio non è ovvio e non è unico per ogni settore o per ogni persona.
In ecologia per esempio si parla di rischio considerando un evento o una attività che può avere un impatto negativo sull’ambiente: inquinamento, introduzione di specie aliene, perdita di biodiversità ecc.
Se chiediamo ad un ingegnere il rischio è una condizione di incertezza che dobbiamo prevedere e quantificare per calcolare correttamente le strutture che stiamo costruendo: la forza del vento, la possibilità di un uragano, la quantità di neve o di pioggia ecc.
Se guardiamo alla sicurezza e alla salute sul lavoro il rischio è la combinazione tra un evento pericoloso e la gravità delle sue conseguenze: se un evento è molto probabile ma poco dannoso è meno pericoloso di un evento raro ma disastroso.
Se guardiamo alla finanza il rischio è la possibilità di perdita di tutto o di parte del capitale. Ma qualcuno può essere più propenso a rischiare altri invece non lo sono affatto.
Gli esempi riportati hanno qualcosa in comune: noi normalmente vediamo il rischio come la possibilità che un evento negativo accada. Questo evento può essere immaginato o essere sconosciuto, essere ricorrente o inaspettato ma noi tendiamo a farlo rientrare all’interno di un nostro modello mentale, statistico, matematico.
Quello che cerchiamo di fare di solito, per fronteggiarlo, è assegnargli una probabilità di accadimento e un grado di dannosità nel caso accada.
Trovo curioso e interessante che il concetto di probabilità e tutta la branca della matematica formale relativa nasca dall’analisi dei giochi di azzardo. A dimostrazione che perfino i matematici, apparentemente algidi, sono immersi nel mondo come tutti noi.
Seppur alcune tracce vengono fatte risalire fino all’antichità, è nel XVI secolo che un medico e matematico italiano Gerolamo Cardano scrive un libro sui “Giochi di fortuna”. Da quel momento, secolo dopo secolo, eminenti matematici si sono cimentati nell’analizzare i giochi di azzardo e formalizzare matematicamente le loro intuizioni e scoperte: Fermat, Pascal, Huygens (che stampò il primo libro sul “Ragionamento nei giochi di fortuna”), Bernoulli (“L’arte della congettura”), de Moivre e infine Laplace che all’inizio del 1800 consolidò le idee precedenti e introdusse nuove tecniche (“Teoria analitica delle probabilità”).
La teoria delle probabilità è semplicemente il buon senso ridotto a calcolo.
Pierre-Simon Laplace
Naturalmente da Laplace nulla si è fermato. Le tecniche si sono consolidate, ma, non soddisfatti, si sono succeduti centinaia di matematici e scienziati che hanno tentato, in svariati modi e con una ampio portafoglio di tecniche, di diventare ricchi con la comprensione dei giochi di azzardo.
È una storia interessante e divertente, con moltissimi aneddoti veramente succulenti, alcuni dei quali magari li vedremo per scoprire modi di ragionare che possono tornare utili a tutti noi.
È mia convinzione che i giochi di azzardo e le tecniche matematiche che ne sono derivate descrivono solo una parte del mondo del rischio. Le probabilità non ci danno sempre la risposta sia perché l’evento successivo è comunque aleatorio sia perché, in molti casi, non sono lo strumento adatto.
Facciamo l’esempio del rischio climatico. Chi potrebbe, dando un numero, calcolare la probabilità di accadimento dell’estinzione della specie umana a causa delle variazioni del clima? Possiamo immaginare scenari, tracciare percorsi, ipotizzare le conseguenze ma non dare una probabilità. Questa indeterminatezza è forse una tra le cause del negazionismo climatico.
Non possiamo essere certi di nulla, ma possiamo essere sicuri che la probabilità ci aiuta a navigare nell'incertezza.
Daniel Kahneman
Ma anche quando le percentuali sono rilevabili dall’esperienza quello che abbiamo di fronte rimane spesso un rischio assoluto. Diciamo che mi piacerebbe provare il base jumping. Mi informo e salta fuori che nello 0,001% dei casi (1 caso su 100.000) il paracadute non si apre (non è un dato vero è solo un esempio!!). È una percentuale ridicola. Se giocassi a tombola non lo guarderei neanche. Però dal momento che non gioco a tombola ma faccio base jumping mettendo a rischio la vita, cosa mi dice quella percentuale? Mi da informazioni utili per farlo oppure no? Qualunque lancio futuro potrebbe essere quel 1 su 100.000. Alla fine la scelta, in questo caso, non sarà fatta su base razionale ma solo emotiva.
Uno degli strumenti che la matematica ci mette a disposizione è la media. Strumento meraviglioso che ci aiuta a capire il mondo. In media viviamo x anni, in media siamo alti x cm, in media possediamo x euro. Anch’io ripeto sempre che in media i rendimenti dei mercati azionari sono stati del 8-9% annui.
Ma ha sempre senso? Soprattutto ha senso per decidere? Diciamo che devo attraversare un fiume largo 400 metri. Non so nuotare ma mi sono informato che in media è alto 1,50 m. Bene, dico, sono alto 1,70 per cui la mia testa resta fuori, ce la posso fare. Purtroppo a metà fiume c’è una buca profonda 10 metri e larga 10 metri che fa media con i 30 cm di profondità dei primi 150 metri. Annego. La media è utile ma non è sufficiente.
La media è un concetto potente, ma può anche essere fuorviante se non si considera la variabilità dei dati.
Darrell Huff
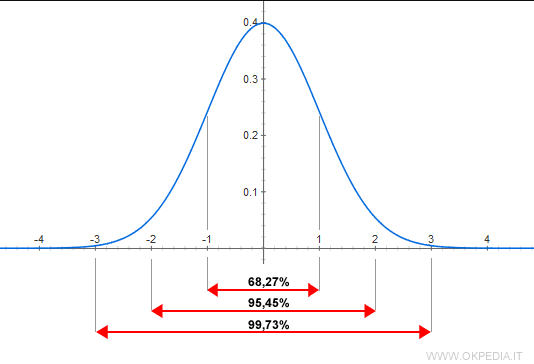
Proprio per questo i matematici e gli statistici dalla media hanno derivato un altro concetto molto usato in una infinità di campi, la distribuzione standard rispetto alla media. È la famosa curva a campana o gaussiana (dal matematico che la introdusse).
Non voglio tediarvi con formule ma il concetto grafico è semplice e potente e, a mio parere va capito.
La verticale centrale rappresenta la media, l’area sotto la linea azzurra rappresenta il numero dei casi che si discostano dalla media.
La curva è molto alta al centro intorno alla media perché sono molti i casi che ricorrono vicini alla media.
Più mi allontano dal centro, più la linea azzurra si abbassa perché sono sempre meno i casi che si discostano molto dalla media, sia in più che in meno.
Nella distribuzione “standard” si dice che il 68,3% dei casi deviano dalla media per 1 “deviazione standard” (σ) (è un concetto statistico ci basti sapere che viene chiamato così). Se ci allontaniamo di 2 deviazioni standard comprendiamo il 95,5% dei casi, in 3 deviazioni standard il 99,73% e così via.
Questa curva spiega molto bene un sacco di fenomeni naturali e biologici: l’altezza di una popolazione, il peso alla nascita, la pressione del sangue si distribuiscono più o meno così.
Veniamo ora ai mercati finanziari accennando a una storia molto interessante. Tre economisti, applicando la distribuzione normale e la deviazione standard hanno inventato una formula per valutare il prezzo delle opzioni1, vincendo per questo il premio Nobel nel 1997. È la famosa formula di Black-Scholes-Merton (il povero Merton è morto prima del conferimento del Nobel per cui spesso non viene citato nella formula).
All’epoca, tra gli investitori professionisti, la formula era sembrata la scoperta più incredibile della storia dell’umanità. Infatti le opzioni esistono fin dall’antica Grecia: Talete di Mileto sembra le abbia usate per arricchirsi. Si proprio quel Talete famoso per i suoi contributi alla geometria, uno dei Sette Sapienti della Grecia antica. Di nuovo finanza e matematica, ça va sans dire.
In ogni caso fino ai primi anni ‘90 non era mai esistito un sistema formale per quantificare il valore di una opzione. Il mondo finanziario, sempre a caccia di qualcosa di nuovo e stupefacente la salutò e applicò la formula di Black & Sholes come fosse la pietra filosofale.
Sholes era talmente convinto della validità della loro intuizione che partecipò alla fondazione e alla gestione di un Hedge-Fund, il Long-Term Capital Management (LTCM) che si basava sull’applicazione di quella formula per l’acquisto e la vendita delle opzioni.
È una storia da raccontare nel dettaglio ma per il momento ci basti sapere che dopo un po’ di anni di successi stratosferici, nel 1998 il LTCM trascinò il mondo finanziario globale sull’orlo del collasso tanto che la FED (la banca centrale americana) costrinse un consorzio di banche ad intervenire accollandosi l’immenso debito accumulato.
Insomma, con questo aneddoto voglio accennare al fatto che con i mercati finanziari le medie , la deviazione standard ecc. non funzionano, o se lo fanno, lo fanno per periodi di tempo relativamente brevi e di mercati “calmi”.
Noi facciamo di tutto per trovare strumenti che ci permettano di domare l’incertezza perché quello che ci disturba non è tanto il rischio in sé ma la variabilità dei risultati. Ci piacerebbe vivere in un un mondo mediocre, dove tutto è certo o prevedibile. Purtroppo non è così. Nassim Taleb famoso studioso, oltre che operatore di borsa, che ha avuto ed ha ampissima fama per aver scritto “Il Cigno Nero”, libro che riflette proprio sui concetti che stiamo esplorando qui, parla di due mondi diversi: il Mediocristan e l’Estremistan. Secondo lui viviamo nell’Estremistan e il Mediocristan è solo il tentativo degli umani di addomesticare il caso. Ma è una specie di autoinganno che ci mette in pericolo perché ci spinge a non adottare le scelte corrette.
"La probabilità è l'unico strumento che abbiamo per affrontare l'incertezza, ma non è una scienza esatta, è un'arte."
Nassim Nicholas Taleb
Per il momento ci fermiamo qua. Nelle prossime puntate cercheremo di capire meglio perché la statistica normale non ottiene grandi risultati nel mondo degli investimenti e come il rischio, o meglio la variabilità dei risultati, oltre ad essere una misura della potenziale perdita è, al contrario, un elemento che può tornare a nostro vantaggio .
Se non sei ancora iscritto alla newsletter è il momento di farlo:
Se pensi che la newsletter possa interessare anche altre persone che conosci, condividila:
Le opzioni sono uno strumento finanziario che permette di acquistare ad un certo prezzo il diritto (non l’obbligo) di comprare una certa quantità di qualcosa (il sottostante) ad un certo prezzo fissato oggi (prezzo strike) ad una certa scadenza futura. Per esempio: compro oggi una opzione a 2 euro per comprare tra 3 mesi un quintale di banane a 100 euro. Se tra 3 mesi il prezzo delle banane è 120 , esercito l’opzione, acquisto le banane a 100 e le rivendo a 120 ottenendo un guadagno di 18 (120-100-2). Se, al contrario, tra 3 mesi il prezzo della banane è 80, avrò perso i 2 euro.